| Original | Transliteration | Translation | |
| Title | সম্ভবত | Sombhoboto | Probably |
| Subtitle | গণনাতত্ত্ব ও সম্ভাব্যতার গণিত | Gononatotto O Sombhabbotar Gonit | Combinatorics & Probability |
Language: Bengali
Pages: 248
Binding: Hardcover
Type of work: Monograph, Original
Subject matter: Popular mathematics
Contributions of Saumitra Chakravarty: Author, Cover-designer, Illustrator
First publication: January 2016
Publisher: Anupam Prokashani, 38/4 Banglabazar, Dhaka-1100, Bangladesh
Online shopping: rokomari.com (within Bangladesh), goodreads.com
International distributors:
- USA
- Muktodhara (মুক্তধারা): 39-25 65 Street, 2E Woodside, New York 11377, Phone # +1-718-458-3616
- Abosar (অবসর): Jackson Heights, New York 11372, Phone # +1-718-397-8173
- UK
- Ruposhi Bangla (রূপসী বাংলা): 220 Tooting High Street, London SW17 OSG, Phone # 020-181-672-7843
- Sangeeta Ltd. (সঙ্গীতা লিমিটেড): 22 Brick Lane, London
- India
- Naya Udyog (নয়া উদ্যোগ): 206 Bidhan Sarani, Kolkata 700006, Phone # +91-33-2241-3540, Mobile # +91-943-345-7210, Email – nayaudyog@yahoo.in
- Abhijan (অভিযান): 10/2-A Ramanath Mazumdar Street, Kolkata 700009, Mobile # +91-801-709-0655
- Sonar Bangla Prakashani (সোনার বাংলা প্রকাশনী): 45 Ratu Sarkar Lane, Kolkata 700073, Mobile # +91-990-325-2109; +91-990-348-2741
Synopsis:
The book is divided into two chapters, the first one is on ‘Combinatorics’ and the second one is on ‘Probability’. It covers the basics of both of the branches of mathematics. The book is intended to provide deep insights into the matter as well as prepare a student to compete in National Math Olympiad and such competitions. Also, anyone with a genuine interest in mathematics will find something new and intersting in the book. The book tries to relate the abstract mathematical concepts of combinatorics and probability to our day-to-day life, and thus may act as an eye-opener. It will ‘probably’ change your world-view.
Excerpts:
Supporting materials:
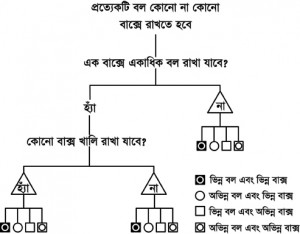
Section 1.26 – Partition
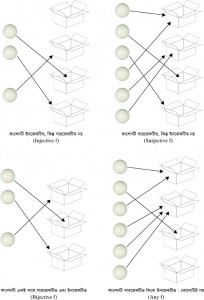
Section 1.28 – Twelvefold Ways Simulator [still working on it…]
Section 2.2 – Cointoss Simulation to Count Heads and Tails
Section 2.6 – Birthday Problem
Section 2.12 – Proabilistic Determination of the Value of e by Shuffling
Section 2.18 – Bernoulli Trial
Section 2.23 – Bayes Theorem
Section 2.28 – Expected Sequence Length Simulator of Cointoss and DNA
Section 2.29 – Birthday Line; Expected Value vs. Trial Length
Section 2.30 – Continuous Probability